Le calcul de la surface de Dieu, par Alfred Jarry...
Voici ce que dit l'article Wikipédia à ce sujet (extrait) :
« Le postulat de départ est aussi de calculer une surface plane, à partir du triangle, représentation symbolique traditionnelle de Dieu. Cependant, pour Faustroll, la trinité divine est davantage contenue dans les trois hauteurs du triangle que dans ses côtés ou sommets.
Dieu est donc supposé sous la figure de trois segments égaux, de longueur a et issus d'un même point.
Soit x la médiane prolongement d'une des personnes a, 2y le côté du triangle auquel elle est perpendiculaire, N et P les prolongements à l'infini, de part et d'autre de la droite (a + x).
or
et
d'où
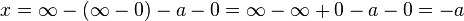 .
.
D'autre part, un triangle rectangle aux côtés a, x et y donne
puisque
d'où
et
La surface du triangle équilatéral sera
Faustroll affirme qu'à première vue du radical 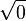 , la « surface » calculée est « une ligne » au plus, et constate que « la base [du] triangle coïncide avec son sommet ». Et de conclure que a est une droite qui joint 0 à
, la « surface » calculée est « une ligne » au plus, et constate que « la base [du] triangle coïncide avec son sommet ». Et de conclure que a est une droite qui joint 0 à  . Autrement dit : « Dieu est le plus court chemin de zéro à l'infini, dans un sens ou dans l'autre ».
. Autrement dit : « Dieu est le plus court chemin de zéro à l'infini, dans un sens ou dans l'autre ».
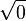 , la « surface » calculée est « une ligne » au plus, et constate que « la base [du] triangle coïncide avec son sommet ». Et de conclure que a est une droite qui joint 0 à
, la « surface » calculée est « une ligne » au plus, et constate que « la base [du] triangle coïncide avec son sommet ». Et de conclure que a est une droite qui joint 0 à  . Autrement dit : « Dieu est le plus court chemin de zéro à l'infini, dans un sens ou dans l'autre ».
. Autrement dit : « Dieu est le plus court chemin de zéro à l'infini, dans un sens ou dans l'autre ».
Mais, Dieu étant inétendu n'est pas une ligne, et dans l'identité 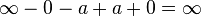 la longueur a n'est pas une ligne mais un point. La conclusion du calcul de la surface de Dieu sera donc, conformément à la formule du Docteur Faustroll : « Dieu est le point tangent de zéro et de l'infini. »
la longueur a n'est pas une ligne mais un point. La conclusion du calcul de la surface de Dieu sera donc, conformément à la formule du Docteur Faustroll : « Dieu est le point tangent de zéro et de l'infini. »
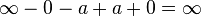 la longueur a n'est pas une ligne mais un point. La conclusion du calcul de la surface de Dieu sera donc, conformément à la formule du Docteur Faustroll : « Dieu est le point tangent de zéro et de l'infini. »
la longueur a n'est pas une ligne mais un point. La conclusion du calcul de la surface de Dieu sera donc, conformément à la formule du Docteur Faustroll : « Dieu est le point tangent de zéro et de l'infini. »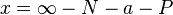

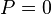



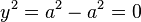


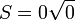
Aucun commentaire:
Enregistrer un commentaire